| Definitions | t  T, FairFifo, World, #$n, r - s, time(e), n+m, loc(e), s(i;t).x, f(a), T, FairFifo, World, #$n, r - s, time(e), n+m, loc(e), s(i;t).x, f(a),  x.A(x), <a, b>, val(e), w-machine(w;i), t.2, t.1, w-pred(w;e), w-info(w;e), when-after(e;info;pred?;init;Trans;val;time), w.T, x.A(x), <a, b>, val(e), w-machine(w;i), t.2, t.1, w-pred(w;e), w-info(w;e), when-after(e;info;pred?;init;Trans;val;time), w.T, 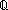 , x:A , x:A  B(x), Id, x:A B(x), Id, x:A  B(x), s = t, A B(x), s = t, A  B, P B, P   Q, E, Q, E,  x:A. B(x), x:A. B(x),  , False, , False,  A, A,  , {x:A| B(x)} , {T}, SQType(T), a < b, i , {x:A| B(x)} , {T}, SQType(T), a < b, i 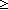 j , Void, -n, n - m, j , Void, -n, n - m,  , r + s, a(i;t), val(a), kind(a), vartype(i;x), loc(e), s ~ t, , r + s, a(i;t), val(a), kind(a), vartype(i;x), loc(e), s ~ t,  b, let x,y,z = a in t(x;y;z), w-automaton(T;TA;M), w.M, w.TA, P & Q, A c b, let x,y,z = a in t(x;y;z), w-automaton(T;TA;M), w.M, w.TA, P & Q, A c B, w-machine-constraint(w), valtype(i;a), B, w-machine-constraint(w), valtype(i;a),  x:A. B(x), Msg(M), type List, isnull(a), IdLnk, Type, kindcase(k; a.f(a); l,t.g(l;t) ), True, tag(k), lnk(k), act(k), islocal(k), left + right, Knd, Unit, if b then t else f fi , S x:A. B(x), Msg(M), type List, isnull(a), IdLnk, Type, kindcase(k; a.f(a); l,t.g(l;t) ), True, tag(k), lnk(k), act(k), islocal(k), left + right, Knd, Unit, if b then t else f fi , S  T, suptype(S; T), outl(x), isl(x), P T, suptype(S; T), outl(x), isl(x), P    Q, first(e), Q, first(e),  , ,   b, s+r, let x = a in b(x), P b, s+r, let x = a in b(x), P   Q, Q,  T, act(e), kind(e), V(i;k), kind(e), case b of inl(x) => s(x) | inr(y) => t(y), Atom$n, x,y:A//B(x;y), T, act(e), kind(e), V(i;k), kind(e), case b of inl(x) => s(x) | inr(y) => t(y), Atom$n, x,y:A//B(x;y),   x,y. t(x;y), qeq(r;s), tt, EquivRel(T;x,y.E(x;y)), A x,y. t(x;y), qeq(r;s), tt, EquivRel(T;x,y.E(x;y)), A 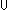 B, B,   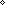 , pred(e), let x,y = A in B(x;y), r * s, , pred(e), let x,y = A in B(x;y), r * s,   x. t(x) x. t(x) |
| Lemmas | IdLnk wf, w-kind wf, kindcase wf, qmul wf, qmul over plus qrng, qadd-add, w-pred-null, false wf, w-loc-pred, w-pred-decreases, pred wf, qadd assoc, mon assoc q, qmul one qrng, qsub wf, int nzero wf, b-union wf, btrue wf, qeq wf2, quotient wf, w-ekind wf, Knd wf, w-V wf, w-eval wf, w-info wf, kind wf, w-kind-lemma, int-rational, qadd wf, int inc rationals, Id wf, rationals wf, w-vartype wf, mon ident q, qadd ac 1 q, qadd comm q, true wf, squash wf, qmul zero qrng, w-first-null, w-stutter, not wf, bnot wf, bool wf, w-pred wf, first wf, assert of bnot, eqff to assert, iff transitivity, eqtt to assert, isl wf, outl wf, actof wf, w-s wf, w-val wf, subtype rel self, assert wf, w-isnull wf, w-a wf, w-machine wf, w-automaton wf, w-T wf, w-TA wf, w-M wf, ge wf, nat properties, nat wf, le wf, w-time wf, w-E wf, Id sq, w-loc-lemma, w-loc wf, world wf, fair-fifo wf |